プログラミング言語Amberの紹介(その1)

3年ぶりに更新します。この３年間にも(途中1年以上別の事をやっていましたが)自作の言語とその処理系の開発は続けていました。そろそろ紹介記事を書き始めようと思います。ホームページは既にありますが、こちらは昨年の夏から更新していないので内容が古くなっています。本記事を元にして後で更新します。

言語の名前はAmberと言います。Amberとは日本語で琥珀という意味です。実は同名の言語処理系がいくつか存在するのですが(larsivi / amber / wiki / Home — Bitbucket, GitHub - eknkc/amber: Amber is an elegant templating engine for Go Programming Language, inspired from HAML and Jade, The Amber Programming Languageなど)、この名前には愛着がありますし、ある先生につけて頂いた名前であるということもあるので私も使用させて頂きます。

Amberは動的型のスクリプト言語で、以下の様な特徴を持ちます。

1. 同図象性
2. データ表現は関数子 + 引数
3. プロトタイプベースのオブジェクトシステム
4. 関数は全て部分関数であり関数同士は合併可能

同図象性とはプログラムとコードが同じ表現を持つという性質でLisp系言語に見られるものです。但し、データ表現はコンスセルではなく、関数子fと幾つかの引数e1,e2,...,enからなる f{e1, e2, ..., en} という形式です。同図象性とプロトタイプベースというのはメタプログラミングを強く意識した選択です。Amberは生成的プログラミングや自己反映的プログラミングなどを非常に平易に行えるように作られています。メタプログラミングを重視する事の具体的な目的はまた後で説明します。Amberの関数は引数のパターン及びガード節によってその定義域を限定される事で部分関数となり、さらに部分同士を合併する事によってあらたな関数を作る事が出来ます。

バグの報告やアイデア・ご意見をいただけますと大変ありがたいです。その場合は[twitter:@9_ties]にお願いします。Amberの仕様はまだ収束していないので細かな変更が今後も続きます。この文書は最新の仕様に合わせるよう頑張りますが、間違っていたらすみません。

ビルド・インストール

Amberのインタプリタamberは以下の手順でビルド・インストールできます。ビルドにはLinux環境とgit,make,binutilsが必要です。デフォルトでは/usr/lib/amber/以下にライブラリ群が、/usr/bin/以下にamberというスクリプト1つがインストールされます。コンフィギュレーションファイルはまだ用意していないので、お手数ですが必要ならばMakefile他を書き直して下さい。インストール先は/usr/lib/またはLD_LIBRARY_PATHに設定されたディレクトリにしてください。

% git clone https://github.com/nineties/amber.git
% cd amber
% make
% sudo make install

ビルドは以下の手順でブートストラッピングにより行われます。

1. アセンブリ言語で書かれたrlcという簡単な手続き型言語のコンパイラをGNU Assemblerでコンパイル。
2. rlcでrlciという簡単なLispインタプリタをコンパイル。
3. rlciでrlvmというamberの仮想マシンのアセンブリコードを生成し、GNU Assemblerでコンパイル。
4. rlciでrlvmのバイトコード用のリンカ(これ自体もrlvm上で動く)をコンパイル。
5. rlciでrlvmのバイトコード用の逆アセンブラ(これ自体もrlvm上で動く)をコンパイル。
6. rlciでamberのソースコードをコンパイルし、rlvm用のオブジェクトファイル(*.rlo)を生成。
7. 上で作成したリンカを使って*.rloをリンク。

Hello World

% amber

でamberのシェルが起動します。(注:まだreadlineやhistoryを実装していませんので行編集が出来ません。そのうち実装します。)
もしくはファイルにプログラムを書いて

% amber hoge.ab

と実行します。Amberスクリプトの拡張子は.abです。

まずはHello Worldです。

amber:1> puts("Hello Amber!")
Hello Amber!
=> nil

シェルを終了させる為にはexitとタイプします。

他にも幾つか見てみましょう。amberシェルでは直前の計算結果を$で参照する事が出来ます。またn番目のプロンプト(amber:n> ...)の結果を$nで取り出せます。例えば以下の2 * $では 2×3を、$2 / $3では3割る6を計算しています。

amber:2> 1 + 2
=> 3
amber:3> 2 * $
=> 6
amber:4> $2 / $3
=> 0.5

また、整数は桁があふれると自動的に多倍長整数に変換されます。

amber:5> 7 ^ 160
=> 1643184774938171857917000410556544806341837419599523497069764671233207565562287891877564323818254449486910838997871467298047369612896001

基本的な数学関数は実装してありますので、とりあえず関数電卓としてそこそこ使えると思います。

amber:6> import math
=> Module{math}
amber:7> math::sin(1)
=> 0.8414709848078965

モジュール変数は :: という記号を使って参照します。importのオプションで指定して現在の名前空間に持ってくる事も出来ます。例えば以下の様にするとmath::なしでsqrtを呼べます。

amber:8> import math (sqrt)
=> Module{math}
amber:9> sqrt(2)
=> 1.414213562373095

他にもある特定の変数以外を持ってきたり、全て持ってくるといった事が出来ます。

amber:10> import math hiding (tan, cos)
=> Module{math}
amber:11> log(2)
=> 0.6931471805599454
amber:12> cos(1)
Exception: UndefinedVariable{cos}
amber:12> import math (*)
=> Module{math}
amber:13> cos(1)
=> 0.5403023058681398

シンボルは変数名などの各種「名称」を表すデータ型です。Amberの識別子([A-Za-z_][A-Za-z0-9_]*[!?]?という文法)に対応するシンボルはシングルクオートで以下の様に記述すると作成出来ます。

amber:14> 'this_is_a_symbol
=> this_is_a_symbol

一般の文字列についてはto_symメソッドでシンボル化できます。

amber:15> "this is a symbol".to_sym()
=> this is a symbol

シンボルは表に登録され、同じ文字列に対応するシンボルは常にメモリ上で同一のデータである事が保証されます。同じ値か否かは演算子 == で、データの実体が同一か否かは関数identical?で調べられます。

amber:16> "abc" == "abc"
=> true
amber:17> identical?("abc", "abc")
=> false
amber:18> 'abc == 'abc
=> true
amber:19> identical?('abc, 'abc)
=> true

その他、原始的なデータ型には真偽値true,falseと意味の無い値である事を表すnilがあります。

派生型の例としてコンテナを紹介します。良く使うコンテナ型はタプル・リスト・配列・テーブル(ハッシュ表)です。演算子[ ]で各要素にアクセス出来ます。その他コンテナの特徴に応じたメソッドが用意されています。

amber:20> (1,2,3)
=> (1, 2, 3)
amber:21> [1,2,3,4,5]
=> [1, 2, 3, 4, 5]
amber:22> Array{1, 2, "foo", "bar"}
=> Array{1, 2, "foo", "bar"}
amber:23> Table{("one", 1), ("two", 2), ("three", 3)}
=> Table{("three", 3), ("two", 2), ("one", 1)}
amber:24> $["two"]
=> 2

変数を定義する場合には := という記号を用います。多くのスクリプト言語ではいきなり変数に代入が出来ますが、Amberでは定義が必要です。

amber:25> x := 2
=> 2
amber:26> x + 1
=> 3
amber:27> x = 3
=> 3
amber:28> x
=> 3
amber:29> y = 1
Exception: UndefinedVariable{y}

制御構造はif文, while文, for文, try-catch文など手続き型言語の標準的なものが実装されています。複数行のコードブロックは { ... } で囲みます。

amber:29> if [1,5,3,4].include?(3) {
amber:29~       puts("found")
amber:29~ } else {
amber:29~       puts("not found")
amber:29~ }
found
=> nil
amber:30> i := 0
=> 0
amber:31> while (i < 10)
amber:31~       i += 1
=> nil
amber:32> i
=> 10
amber:33> for i in 1..10
amber:33~       puts i
1
2
3
4
5
6
7
8
9
10
=> nil
amber:34> for v in [1,2,3,4]
amber:34~       puts v
1
2
3
4
=> nil

あとはshift-resetベースの限定継続を実験的に実装しています。Amberのアプリケーションでは対話型セッションを積極的に使っていこうと思っているので継続はあった方が良いだろうという考えです。ただ、これを実装する可能性を考えずにガベージコレクタを実装してしまったので、大分実装が面倒な事になってしまいました。実装にあたっては以下を参考にさせて頂きました。
益子萌,浅井健一(2009)「MinCamlコンパイラにおけるshift=resetの実装」PPL09

amber:35> cont := nil
=> nil
amber:36> reset () -> {
amber:36~       puts("foo")
amber:36~       shift k -> { cont = k }
amber:36~       puts("bar")
amber:36~       shift k -> { cont = k }
amber:36~       puts("baz")
amber:36~ }
foo
=> <#Function>
amber:37> cont(nil)
bar
=> <#Function>
amber:38> cont(nil)
baz
=> nil

データの表現

Amberのデータは数値型や文字列型などの原始的オブジェクト(アトム)と、シンボルfと幾つかの引数e1,e2,...,enからなるf{e1, e2, ..., en}という形式の派生オブジェクトからなります。Amberではfをオブジェクトのヘッド、nをアリティと呼んでいます。(アリティはヘッドの属性ではなくてオブジェクトの属性です。通常の用法と異なるので奇妙かもしれませんが、他に良い名前が思い浮かびませんでした。)
fullformという関数で任意のオブジェクトをこの形式で文字列化する事ができます。また、.head, .arity, .argumentsでそれぞれを取り出す事が出来ます。(fullformという呼称はMathematicaから頂いています。)

amber:39> obj := (1,2,[3,4])
=> (1, 2, [3, 4])
amber:40> fullform(obj)
=> "Tuple{1, 2, List{3, 4}}"
amber:41> obj.head
=> Tuple
amber:42> obj.arity
=> 3
amber:43> obj.arguments
=> [1, 2, [3, 4]]

もちろん、fullformを直に入力しても良いです。

amber:44> List{1, List{2, 3}, List{4, 5}}
=> [1, [2, 3], [4, 5]]

アトムは派生オブジェクトではないのでfullformはありませんが、これらにもヘッドと呼ばれるシンボルが紐付けられておりアリティが0のオブジェクトとして派生オブジェクトと同様に取り扱う事が出来ます。

amber:45> "abc".head
=> String
amber:46> "abc".arity
=> 0
amber:47> "abc".arguments
=> []
amber:48> fullform("abc")
=> "\"abc\""

同図象性

Amberのプログラムそれ自体をAmberのデータとして取り扱う事が出来ます。Lispと同様にクオート(記号')を利用すると評価器の評価を止めて構文木を取り出す事が出来ます。出力は整形されますが、fullformを使えば通常のデータと同じ構造である事が判ります。また、関数evalfullによってそれを評価する事が出来ます。

amber:49> '{
amber:49~       s := 0
amber:49~       for i in 1..100
amber:49~               s += i^2
amber:49~       s
amber:49~ }
=> {
       s := 0
       for i in 1..100 {
           s += i^2
       }
       s
   }
amber:50> fullform($)
=> "Block{Define{s, 0}, For{i, Range{1, 100}, Block{AddAssign{s, Pow{i, 2}}}}, s}"
amber:51> evalfull($49)
=> 338350

準クオート(記号`)とアンクオート(記号!)も用意されていて、準クオートの中ではアンクオートされた部分だけ評価が行われます。

amber:52> `(1 + !(2 + 3))
=> 1 + 5

関数

関数も記号 := を用いて定義します。

amber:53> f(x) := x + 1
=> <#Function>
amber:54> f(1)
=> 2

関数の引数部には各種パターンを指定する事が出来ます。例えば定義域を整数のみに限定した部分関数は以下の様に定義します。この関数に整数以外を渡すとMatchingFailed例外となります。

amber:55> g(x @ Int) := x + 1
=> <#Function>
amber:56> g(1)
=> 2
amber:57> g(1.5)
Exception: MatchingFailed{domain = (x @ Int), [1.5]}

引数部に何らかのフォームを書くともっと複雑なパターンマッチングが出来ます。

amber:57> g(Foo{x, y}) := (x, y)
=> <#Function>
amber:58> g('Foo{1, 2})
=> (1, 2)
amber:59> g(x + y) := (x, y)
=> <#Function>
amber:60> g('(2 + 3))
=> (2, 3)

以下Amberで使用する事が出来るパターンを列挙していきます。

DontCareパターン(記号_)

amber:61> g([_, _, x, _]) := x
=> <#Function>
amber:62> g([1,2,3,4])
=> 3

リテラルパターン(定数値)

amber:63> g(0) := "zero"
=> <#Function>
amber:64> g(0)
=> "zero"
amber:65> g('[x,y,z]) := "matched"
=> <#Function>
amber:66> g('[x,y,z])
=> "matched"

可変長パターン(記号...)

amber:67> g(Foo{_, _, ...}) := "Foo object with arity >= 2"
=> <#Function>
amber:68> g('Foo{1, 2, 3})
=> "Foo object with arity >= 2"
amber:69> g('Foo{1})
Exception: MatchingFailed{domain = (Foo{_, _, ...}) | ('[x, y, z]) | (0) | ([_, _, x, _]) | (x + y) | (Foo{x, y}) | (x @ Int), [Foo{1}]}
amber:69> g([_, _, rest...]) := rest
=> <#Function>
amber:70> g([1,2,3,4,5,6])
=> [3, 4, 5, 6]

ガード節

amber:71> g(x) when x > 0 := "positive value"
=> <#Function>
amber:72> g(1)
=> "positive value"

ORパターン

amber:73> g(_ @ Int or _ @ Float) := "a number"
=> <#Function>
amber:74> g(1)
=> "a number"
amber:75> g(1.0)
=> "a number"

あと、パターンではないのですが、キーワード引数が使えます。

amber:76> g(x = 0, y = 1) := (x, y)
=> <#Function>
amber:77> g(x = 1, y = 2)
=> (1, 2)
amber:78> g(y = 3)
=> (0, 3)

この時、gという名前で定義された全ての関数は次々に合併され、一つの関数になっています。現在gの定義域がどのようになっているかは次のようにして見ることが出来ます。

amber:79> g.domain
=> domain = (x = 0, y = 1)
          | (_ @ Int or _ @ Float)
          | (x) when x > 0
          | ([_, _, rest...])
          | (Foo{_, _, ...})
          | ('[x, y, z])
          | (0)
          | ([_, _, x, _])
          | (x + y)
          | (Foo{x, y})
          | (x @ Int)

gに渡された値はdomainの上から順番にチェックされ最初にマッチした関数の実体が呼ばれます。(実際には実行時に多少の最適化が行われて動的にマッチングを行うバイトコードが生成されています。)

上の例を見れば分かるように常に最後に定義されたものが優先されるので、一般的な場合を先に定義し特殊な場合を後に書きます。例えばフィボナッチ数を返す関数fibは以下のように書くことが出来ます。

amber:80> fib(n) := fib(n-1) + fib(n-2)
=> <#Function>
amber:81> fib(0) := 0
=> <#Function>
amber:82> fib(1) := 1
=> <#Function>
amber:83> fib(20)
=> 6765

変数定義が増えてきたので一旦初期化しましょう。

amber:84> .clear()
=> nil

無名関数は以下のようにして作る事が出来ます。

amber:85> (x, y) -> x + y
=> <#Function>
amber:86> $(2, 3)
=> 5

1引数の関数は非常に良く使うので、1引数の時だけは引数の括弧を省く事が出来ます。

amber:87> x -> x + 1
=> <#Function>
amber:88> $(1)
=> 2

Amberの関数はファーストクラスオブジェクトなので他の関数に渡す事が出来ます。

amber:89> [1,2,3,4].map(x -> x + 1)
=> [2, 3, 4, 5]

関数f,gの合併は演算子|によって行う事が出来ます。この場合左側の関数がマッチングにおいて高い優先度を持ちます。

amber:90> x @ Int -> "integer" | x @ Float -> "floating point" | x @ String -> "string"
=> <#Function>
amber:91> $.domain
=> domain = (x @ Int)
          | (x @ Float)
          | (x @ String)
amber:92> $90(1)
=> "integer"
amber:93> $90(1.0)
=> "floating point"
amber:94> $90("Hello")
=> "string"

あと、レキシカルスコープのクロージャがあります。

amber:95> make_counter() := {
amber:95~       n := 0
amber:95~       () -> { n += 1 }
amber:95~ }
=> <#Function>
amber:96> cnt1 := make_counter()
=> <#Function>
amber:97> cnt2 := make_counter()
=> <#Function>
amber:98> cnt1()
=> 1
amber:99> cnt1()
=> 2
amber:100> cnt2()
=> 1
amber:101> cnt1()
=> 3
amber:102> cnt2()
=> 2

テンプレートメタプログラミング

演算子[ ]に関数fを渡すとfにマッチする部分を書き換えるという動作をします。

amber:103> obj := 'Foo{1,2,3}
=> Foo{1, 2, 3}
amber:104> obj[ 1 -> 3 | 2 -> 5 ]
=> Foo{3, 5, 3}

1 -> 3 | 2 -> 5の部分が関数ですが、そう見えないよう意図的に文法を作っています。

これを使ってテンプレートメタプログラミングを非常に簡単に実現する事が出来ます。例えば和 f(1) + f(2) + f(3) + ... + f(n) を求める擬似コードは以下のように書けます。

amber:105> '{
amber:105~      s := 0
amber:105~      for i in 1..n
amber:105~              s += f(i)
amber:105~      s
amber:105~ }
=> {
       s := 0
       for i in 1..n {
           s += f(i)
       }
       s
   }

これを先ほどの方法で書き換えれば実行可能なコードを生成する事が出来ます。

amber:106> $[ 'f(i) -> '(1/i^2) | 'n -> 100 ]
=> {
       s := 0
       for i in 1..100 {
           s += 1 / i^2
       }
       s
   }
amber:107> evalfull($)
=> 1.634983900184892

これを元にマクロを作ってみましょう。Amberはフォームをmacroという関数で変換してから評価します。標準では以下のようなフォームに対するマクロが定義されています。

amber:108> macro.domain
=> domain = (e @ Import{mods, asname, option})
          | (DefTrait{head})
          | (DefClass{head, fields})
          | (WithSlots{obj, init})
          | (When{args, guard} -> body)
          | (Domain{args, List} -> body)
          | ((for i in a..b body))
          | ((for i in container body))
          | (ArithAssign{x[idxs...], e, op})
          | (x[idxs...] = e)
          | (x[idxs...])
          | (x |= y)
          | (x %= y)
          | (x //= y)
          | (x /= y)
          | (x ^y)
          | (x **= y)
          | (x *= y)
          | (x -= y)
          | (x ++= y)
          | (x += y)
          | (x <=> y)
          | (x != y)
          | (x == y)
          | (x >= y)
          | (x <= y)
          | (x > y)
          | (x < y)
          | (x | y)
          | (x % y)
          | (x // y)
          | (x / y)
          | (x^y)
          | (x ** y)
          | (x * y)
          | (x ++ y)
          | (x - y)
          | (x + y)
          | (-x)
          | (+x)
          | (|x|)
          | (Assign{Send{obj, f, args}, e, g})
          | (Define{Send{obj, f, args}, e, g})
          | (Assign{Apply{f, args}, e, g})
          | (Define{Apply{f, args}, e, g})
          | (Send{obj, f, args} = e)
          | ((Send{obj, f, args} := e))
          | ((Apply{f, args} := e))
          | (Apply{f, args} = e)
          | (e)

これを拡張して f(1) + f(2) + ... + f(n) を計算するマクロ sum(f, i, n) を作りましょう。"sum"の部分はsumというシンボル自体にマッチして欲しいのでリテラルパターン('sum)を使います。また、テンプレート内で使われている変数sは展開後に名前が衝突しないように、ユニークな名前に先に置き換えておきます。symbolモジュールのunique関数はシンボル表に登録されていない(従って他のシンボルと常に異なる)シンボルを生成します。

amber:109> macro( ('sum)(f, i, n) ) := {
amber:109~      template := '{
amber:109~              s := 0
amber:109~              for i in 1..n
amber:109~                      s += f(i)
amber:109~              s
amber:109~      }
amber:109~      u := symbol::unique()
amber:109~      template['s -> u]['f(i) -> f | 'i -> i | 'n -> n]
amber:109~ }
=> <#Function>

これだけで新しいフォームを使う事が出来ます。sという名前の変数を使っても正しく動作している事が分かると思います。

amber:110> sum(i^2, i, 1000)
=> 333833500
amber:111> sum(1/s, s, 10000)
=> 9.787606036044345
amber:112> sum(sum(i*j, i, j), j, 100)
=> 12920425

Lispでは準クオートを用いてテンプレートを記述する方式が使われますが、私はかねてから埋め込む方式よりも変換する方式の方が理解しやすいのではないかと考えていました。また、上の方式ならば準クオートとアンクオートが用意されていない言語に対してもテンプレートのインスタンシエーションが簡単に出来ます。この方式は標準ライブラリの実装でも使ってみましたが、コードがすっきりとし今の所は良い印象を持っています。準クオート方式と比べたデメリットについてはまだ十分に考察が出来ていません。ちなみに先ほどのマクロを準クオート方式で書くと以下の様になります。

amber:113> macro( ('sum)(f, i, n) ) := {
amber:113~      u := symbol::unique()
amber:113~      `{
amber:113~              !u := 0
amber:113~              for !i in 1..!n
amber:113~                      !u += !f
amber:113~              !u
amber:113~      }
amber:113~ }
=> <#Function>

パーサ生成

前節の方法はAmberのテンプレートでAmberのコードを生成する例でしたのでAmberの文法で全て書くことが出来ました。しかし、他の言語の構文木を作成したい場合にはAmberの文法が使えないので全てfullformで書かなければならなくなってしまいます。そこでパックラット構文解析器のジェネレータが用意されており、Amber内でパーサを作成出来るようになっています。

実はこれまで使ってきたAmberの文法自体もこのジェネレータで書かれています。インタプリタにあらかじめ組み込まれている文法はアトム及びfullformのみで、起動してから自身のパーサをコンパイルする方式になっています。(起動が遅いのは主にこの為です。いずれプリコンパイルにします。)これはlib/syntax/parse.ab内で行われており、最初はfullformのみでコードを書く→文法を定義する為の文法を定義する→Amberの文法を定義する→マクロの仕組みを作る→各種マクロを定義するという流れになっています。

以下はこのジェネレータを使ってCAST(C Abstract Syntax Tree)というC言語風の言語を定義したライブラリの一部です。基本は解析表現文法(PEG)ですが、カンマ区切りのような良く使うパターンをパースする為のdelimitedなどいくつかユーティリティが追加されています。他にも空白の扱いなどが異なるので、解説をAmberのホームページに書くつもりです。

primary_expr ::= identifier      { Var.new($0) }
               | constant
               | string          { StringL.new($0) }
               | "(" expr ")"    { $1 }

postfix_expr ::= postfix_expr "[" expr "]"
                 { Subscript.new($0, $2) }
               | postfix_expr "(" delimited(assign_expr, ",") ")"
                 { Call.new($0, $2) }
               | postfix_expr "." identifier
                 { Select.new($0, $2) }
               | postfix_expr "->" identifier
                 { Select.new(Deref.new($0), $2) }
               | postfix_expr "++"
                 { PostInc.new($0) }
               | postfix_expr "--"
                 { PostDec.new($0) }
               | primary_expr

Amberのシェルから以下のように使えます。

amber:114> import CAST
=> Module{CAST}
amber:115> template := '<CAST>{
amber:115~      struct hoge {
amber:115~              int x;
amber:115~              double y;
amber:115~      }
amber:115~      int main(int argc, char **argv) {
amber:115~              struct hoge st;
amber:115~              st.x = 0;
amber:115~              st.y = 2.0;
amber:115~              printf("%d, %f\n", st.x, st.y);
amber:115~      }
amber:115~ }
=> CASTProgram{[DefAggregates{none, StructT{hoge}, hoge, [(int, x), (double, y)]},
    DefFunc{none, int, main, [(int, argc), (PointerT{PointerT{char}}, argv)], {
        [DefVar{none, StructT{hoge}, st, nil}, Select{Var{st}, x} = IntL{0},
         Select{Var{st}, y} = FloatL{2.0},
         Call{Var{printf}, [StringL{"%d, %f\n"}, Select{Var{st}, x},
          Select{Var{st}, y}]}] }}]}

このようなテンプレートはもちろん先ほどと同様に操作する事が出来ます。上ではAmberのコード中に埋め込みましたが、CASTのコードが書かれた外部ファイルをパーズする事も出来ます。あとはファイルにコードを書き出すpretty printerを実装すればCAST -> CASTの変換器が出来上がります。今は実験的な実装ですがいずれちゃんとC言語のパーサを実装します。(PEGでは書けないのでパーサを直に書き下す形になります。) また各種最適化もライブラリ関数として実装する予定です。このライブラリはFFIの実装などで使います。Amberの次期VMの実装にもこれを使い、libc他既存のライブラリを使えるようにするつもりです。

パーサは個々の構文要素が独立した関数として生成されます。

amber:116> syntax::expr
=> <#Function>
amber:117> syntax::stmt.domain
=> domain = (parser @ Parser) when *hidden*
          | (parser @ Parser) when *hidden*
          | (_ @ Parser)

従って、関数合併を使って既存の文法を拡張する事が出来ます。

amber:118> syntax::mystmt ::= "mystatement" "{" stmt "}" { `printf("my statement %p\n", '!$2) }
=> <#Function>
amber:119> syntax::stmt = syntax::mystmt | syntax::stmt
=> <#Function>
amber:120> mystatement{ puts("Hello") }
my statement Apply{puts, ["Hello"]}
=> nil

言語の構文に何らかの拡張を行う場合、パーサ全体が一つの実体として作られている場合にはソースコードに手を入れる必要があります。上の方法ならばソースコードを書き換えずに外側から拡張を追加する事が出来ます。

オブジェクトシステム

Amberにはプロトタイプベースのオブジェクトシステムが実装されています。

1. オブジェクトにはスロットを追加する事が出来る。
2. parentという特別なスロットがあり、参照されたスロットが見つからなかった場合にはparentを見に行く。
3. obj.f(...)という形で関数が呼び出された場合、f内部ではselfによってobjを参照する事が出来る。

amber:121> a := 'Foo{}
=> Foo{}
amber:122> b := 'Bar{}
=> Bar{}
amber:123> a.f() = "self=" ++ str(self)
=> <#Function>
amber:124> b.parent = a
=> Foo{}
amber:125> a.f()
=> "self=Foo{}"
amber:126> b.f()
=> "self=Bar{}"

self.x という形は頻繁に登場するのでselfを省略して.xと書けるようになっています。

amber:127> a.x = 0
=> 0
amber:128> a.g() = puts(.x)
=> <#Function>
amber:129> a.g()
0
=> nil

また, オブジェクトの生成とスロットの追加を一度に行えるように obj with { スロットの初期化 } という構文も作りました。

amber:130> obj := 'Foo{} with {
amber:130~      .x = 1
amber:130~      .y = 2
amber:130~      .f() = .x + .y
amber:130~ }
=> Foo{}
amber:131> obj
=> Foo{}
amber:132> obj.x
=> 1
amber:133> obj.y
=> 2
amber:134> obj.f()
=> 3

親と子が同名の関数を持つ場合、子の関数が親の関数を隠蔽するような実装が多いと思いますが、Amberでは親と子の関数を合併した新たな関数が子に追加されます。例えば以下のようになります。

amber:135> .clear()
=> nil
amber:136> a := 'Foo{} with {
amber:136~      .f(x) = "parent"
amber:136~ }
=> Foo{}
amber:137> b := 'Foo{} with {
amber:137~      .parent = a
amber:137~      .f(0) = "child"
amber:137~ }
=> Foo{}
amber:138> b.f(1)
=> "parent"
amber:139> b.f(0)
=> "child"
amber:140> a.f(0)
=> "parent"

合併したくない場合には、obj.f(...) := という構文を使わないでobj.fに無名関数を代入するように書けばよいです。

これを使って面白い事が出来ます。

amber:141> fib := 'Fib{} with {
amber:141~      .f(n) = .f(n-1) + .f(n-2)
amber:141~      .f(0) = 0
amber:141~      .f(1) = 1
amber:141~ }
=> Fib{}
amber:142> fib2 := 'Fib{} with {
amber:142~      .parent = fib
amber:142~      .f(0) = 1
amber:142~ }
=> Fib{}
amber:143> fib.f(20)
=> 6765
amber:144> fib2.f(20)
=> 10946

fib2ではf(0) = 1以外は親の定義を使って新しい関数を合成しています。.f(n-1) + .f(n-2) の部分で呼び出されるfの実体がselfによって動的に決まるOpen recursionという性質とAmberの関数合併のメカニズムを組合せて使っています。このように「親を一切書き換えずに機能を拡張したバージョンを新たに作る」という事を非常に手軽に実現出来ます。

Amberのモジュールは実は通常のオブジェクトであり上の仕組みが標準ライブラリで実装されています。.push()というメソッドは、現在の変数表の子供を新たに作ります。.pop()は変数表を破棄して親に戻します。これによって.push()から.pop()までの間の差分のみが破棄されます。

amber:145> x := "old version"
=> "old version"
amber:146> .push()
=> nil
amber:147> x := "new version"
=> "new version"
amber:148> .pop()
=> nil
amber:149> x
=> "old version"

以下の様にOpen recursionによって各モジュール変数は常に最新の変数表を参照します。この点がサブスコープを作るのとは異なります。

amber:150> f() := x
=> <#Function>
amber:151> .push()
=> nil
amber:152> x := "new version"
=> "new version"
amber:153> f()
=> "new version"
amber:154> .pop()
=> nil
amber:155> f()
=> "old version"
amber:156> {
amber:156~      x := "new version"
amber:156~      f()
amber:156~ }
=> "old version"

以下の例は、一時的に整数の四則演算を全て有理数の物に置換え、popによってそれを元に戻すという例です。

amber:157> 1/2
=> 0.5
amber:158> .push()
=> nil
amber:159> import algebra::rational (*)
=> Module{rational}
amber:160> 1/2 + 2/3
=> 7 / 6
amber:161> s := 0
=> 0
amber:162> for i in 1..100
amber:162~      s += 1/i
=> nil
amber:163> s
=> 14466636279520351160221518043104131447711 / 2788815009188499086581352357412492142272
amber:164> .pop()
=> nil
amber:165> 3/5
=> 0.6

このようにAmberではオブジェクトシステムをオブジェクト指向の為というよりはむしろ変数の管理に為に導入しています。一応、以下のように原始的なクラスやトレイトは標準ライブラリで用意していますがこちらは低機能です。

amber:166> class Point{x, y}
=> Class{Point}
amber:167> p := Point.new(x = 1, y = 2)
=> Point{1, 2}
amber:168> trait PairLike with {
amber:168~      .to_pair() := (self[0], self[1])
amber:168~ }
=> Trait{PairLike}
amber:169> Point.extend(PairLike)
=> Class{Point}
amber:170> p.to_pair()
=> (1, 2)

紹介その1終わり

その２ではAmberのアプリケーションとして、対話セッションにより短いテンプレートからC言語のコードを生成するという数値計算からの例を紹介したいと思います。

シカゴのブリザードに遭遇した話

現在2カ月の短期滞在研究でアメリカに来ています。一人での海外滞在は初めてです。
さて、その滞在初日から貴重な経験をしたので記録を残しておきます。
日本でもニュースになったらしいシカゴのブリザード(スノーマゲドン)に捕まりました。
(Chicago Tribune)

2/1, 7:50

成田を出てChicago O'Hare International Airport(ORD)に時間通りに到着。そしてNewark Liberty International Airport(EWR)行きに乗り換える予定だったのですが、既に欠航が決まっていました。

チケットの振替をお願いしたのですが、当日便は全て欠航になるらしく翌日の便に変えてもらいました。
というわけでシカゴ泊が決定。自分は以下のようにして宿を確保することができました。

1. まず、職員に相談するとAirport Accommodationと書かれたピンク色のチケット(写真撮り忘れた)をもらえた。これでホテルの部屋が安く取れるという。
2. ロビー備え付けの電話から予約センターに電話(#7)。まず空港名を聞かれる。ピンクのチケットはもらってるか？と聞かれる。次にホテルの候補と金額を言ってくれるので選ぶ(自分は$60のHilton Garden Innを選んだ)。次に名前を聞かれる。相手は日本名のスペルが分からないので、N,A,K,A,M,U,R,Aと一文字ずついう。最後に、ピンクのチケットにホテル名、金額、予約番号を記入するように言われる。
3. ホテルに移動する。ターミナルの入り口前にシャトルバス乗り場があるので、泊まるホテルの名前が書いてあるバスに乗る。大体30分間隔くらいで走っている。
4. ホテルに着いたらピンクのチケットとクレジットカードを受付に渡す。

ホテルに移動するまでの間バスの運転手がいろいろ教えてくれました。まず、今晩は過去に無いくらいの積雪(50センチ)が予想されているということ。明日の空港は多分閉鎖されるだろいうということ。数日は動けないだろいうということ。

2/1, 9:30頃

ホテルではFree WIFIだったので家族等に連絡をし天気予報やフライトの状況などをチェックしました。
そうこうしていると、昼過ぎくらいに突然停電。ネットも通じなくなりました。フロントに行くと人がわんさかいて、コーヒーを飲んで話をしていました。自分は時差ぼけもあって眠かったので、毛布を１つもらって部屋帰って寝ました。

2/1, 18:00頃

起きたら雪が激しくなってました。

停電はまだ続いていました。
お腹がすいたので夕食。予備電源かなんかで調理しているらしく、料理が出てくるのに時間がかかるという説明。40分くらい待ったと思います。
Shrimp Scampiを食べている時にレストランの照明が全部落ちました。隣のロビーはまだ照明が生きていたので、ほんのり明るいというくらいでした。停電の為クレジットカードが使えないので、食事代は部屋代に後で付けるという説明がありました。
インターネット回線が生きていないので自分は状況が分からなかったのですが、携帯電話で情報収集していた中国系アメリカ人の人にいろいろ教えてもらいました。ここいら一体は全部停電してしまっていて今日中には復旧する見込みがないということでした。
それから、空港周辺では2つのホテルだけが電気系統が無事だという事も教えてもらえました。もちろん移動手段はありません。
何もできないので部屋に戻りましたが、時差ぼけで眠れないのでコーディングをするなど。電源は死んでましたが、出発前に予備バッテリーを用意していたのがラッキーでした。

2/1, 22:00頃

突然火災警報がなりました。部屋のスピーカーから大音量で「火災報知機が反応しました。確認中なので待って下さい(Please hold on)」と流れ、少しすると「この付近で火災が発生しました。エレベータは使わないで非常階段から直ちに外に出て、指示に従って下さい。」みたいな感じの放送に変わりました。というわけで慌てて避難。目の前を歩いてた人は裸足。非常階段は電気がついてました。
一階の非常口は外から雪でふさがってて開かないし、とりあえずロビー方向に移動。ロビーには人がわんさか、そして直ぐに消防車が来ました。結局火事ではなくて、電気系統の故障による警報機の誤作動みたいでした。朝まで計4回火災警報がありました。

こんな雪なのに消防車が来れるのは大型の除雪車が夜通し作業しているからのようです。

写真の場所は除雪車がガソリンを補給する場所のようです。
これは自分の部屋から撮った写真。

2/2, 9:00頃

夜中に比べると降雪が減っていました。写真に移っているのはホテルの人で奥に見えるシャトルバスを移動させようとしていました。

ロビーでコーヒーを飲んで暖まっていると、シャトルバスが入り口まで来て従業員の人がアナウンス。「昨晩は停電で不便をかけて申し訳ありませんでした。食事代を除いて昨日の部屋代は頂きません。これから別の電気系統が無事で朝食を取る事が出来るホテル(確か$99のと$85の2つ候補があった)へバスを出します。」というような感じの内容だったと思います。Hilton Garden Innでは朝食の仕入れが出来ていないみたいでした。

自分は$99の方(Embassy Suites)を選んでシャトルバスに乗りました。移動中は真っ白で何も見えず、路肩の雪を削りながら走るような感じでした。途中雪に埋まっている車(もちろん人は乗っていない)が沢山ありました。

(長いので続きは後で書く)

「末尾最適化」を正しく理解する

以下の記事でPythonやRubyの末尾再帰関数をループに変換する手法が「末尾再帰最適化」や「末尾呼び出し最適化」として紹介されているのですが、これらの用語を使うのは間違いです。
紹介されている手法(動的束縛を利用して制御フローを変形する手法)自体は大変面白いですね。
Pythonで末尾再帰最適化をする。
Rubyで末尾再帰最適化をする。

参考文献として以下を挙げておきます。
William D. Clinger "Proper Tail Recursion and Space Efficiency"
ちゃんと読み直していないので、以下の説明に間違いがあるかも知れません。その場合はご指摘お願いします。

まず「末尾呼び出し(Tail Call)」は関数の一番最後の式(末尾式)であって、関数呼び出しであるものを指します。

void foo() {
    bar();
    baz(); /* 末尾呼び出し */
}

末尾呼び出しは再帰呼び出しでなくても良いので、本来は末尾再帰より広い概念です。しかし、末尾最適化が必要になるのはほとんどの場合再帰関数なので、[訂正]関数呼び出しが再帰するか否かを判断する事は困難である(コールグラフの構築が難しい)から、末尾呼び出しを無条件で末尾再帰と呼ぶこともあるようです。

関数を呼び出す際には色々な用途でメモリ確保が発生します。

• 戻り先アドレスをどこかに積む
• 関数引数を確保する
• 呼び出し元のローカル変数を退避する
• 呼び出された関数のローカル変数を確保する
• クロージャの自由変数を確保する

等です。
末尾呼び出しの場合はこれらを除去できるわけですが、どれほど効率的な実装になっているかよっていくつかのクラスに分類されます。

Improper Tail RecursionとProper Tail Recursion

末尾呼び出し時に戻り先の継続を渡すような実装をImproper(誤った) Tail Recursion、生成しない実装をProper(正しい) Tail Recursionと言います。「戻り先の継続を生成して渡す」というのは、大抵の実装では現在の環境(ローカル変数等)を保存し、戻り先アドレスをスタックに積み、関数をコールしてからリターンするようなものを指します。
Improper Tail Recursionでは、環境の確保などをいくら工夫して0にしても戻りアドレスは除去できないので必ずメモリが増加し、いつかメモリが足りなくなります。

一方のProper Tail Recursionは現在の環境を破棄し、関数コールの代わりにただのジャンプを行うような実装を指します。
この場合、一切のメモリの増加を防ぐことができます。

さらに細かいクラス分けについておおざっぱに説明します。

Improper Tail Recursionのクラス

• S-Stack
  • 環境の一部をスタック上に直接確保する実装。
• S-GC
  • 環境をヒープに確保し、ポインタ一つを保存する実装。この場合関数コールから戻らずとも、死んだデータはGCにより解放できるので、S-Stackよりメモリ効率が良いクラスです。

Proper Tail Recursionのクラス

• S-Tail
  • 上で書いたProper Tail Recursionの最低限の条件を満たした実装。
• S-Evlis
  • S-Tailの条件に加え末尾呼び出しをまたいだ環境の退避を除去した実装。ヒープに退避された環境は二度とアクセスされないので、除去できます。
• S-Free
  • S-Tailの条件に加えクロージャ変換を用いる実装。環境の退避が最小限になります。
• S-SFS (Safe for Space)
  • S-Freeに加え、条件分岐などでも変数の生存解析を使う方法。環境の退避がさらに減ります。

さて、一般的には末尾呼び出しをProper Tail Recursionで実装をすることを末尾最適化をすると言います。
上のPythonやRubyの例は関数コールを除去しているわけではないので末尾最適化には該当しません。関数の呼び出し関係を書き換える別種の変換になります。
実際、この方法でも末尾再帰関数であればスタックの増加を防げているわけですが、f(),g(),h(),..と異なる関数を次々と末尾呼び出しするような場合にはスタックの増加を抑える事はできないなどの点で末尾最適化とは異なっています。

Project Euler (74 〜 80) ピタゴラス数、五角数定理、トポロジカルソートなど

今日は80まで。このところ、数学を使う問題が沢山で面白いですね。

ピタゴラス数とブロコット木 Problem75

簡単には

1,500,000以下のLで
a^2 + b^2 = c^2 かつ a + b + c = L
を満たす自然数a,b,cの組がちょうど一組となるようなLの個数を求めよ

という問題です。a^2 + b^2 = c^2を満たす自然数(a,b,c)をピタゴラス数と言います。また、この方程式をピタゴラス方程式と言いますが、ペル方程式などと同じくディオファントス方程式の一種です。
(a,b,c)がピタゴラス数の時kを自然数として(ka,kb,kc)もピタゴラス数なので、(a,b,c)が互いに素であるものについて考えれば良いです。これを原始ピタゴラス数といいます。
さて、原始ピタゴラス数はその生成方法が知られていて

m > n かつ m,nは互いに素 かつ 片方が偶数のとき(m^2-n^2,2mn,m^2+n^2)は原始ピタゴラス数

となります。
これを列挙する時に厄介なのが「m,nが互いに素」の条件ですが、そこでProblem 71, 73でも使ったブロコット木が役に立ちます。
ブロコット木を使うと既約分数を高速に列挙する事ができるわけですが、このとき分子と分母が必ず互いに素になっている性質が使えます。

L = 1500000
$count = {} # 解の個数
def dfs(la,lb,ra,rb)
    # naとnbは互いに素
    na = la + ra
    nb = lb + rb
    c = 0
    if (na+nb)%2 == 1
        l = 2*(na+nb)*nb
        return if l > L
        # 原始ピタゴラス数の倍数をカウント
        (1..L/l).each do |k|
            $count[k*l] || $count[k*l] = 0
            $count[k*l] += 1
        end
    end
    dfs(la,lb,na,nb)
    dfs(na,nb,ra,rb)
end
dfs(0,1,1,1)
count = 0
$count.each_value {|v| count += 1 if v == 1}
puts count

実行時間は1.11sでした。

整数分割、五角数定理(Problem 76, 77, 78)

この3問は整数分割に関する問題です。整数分割とは整数nを自然数の和で表す場合の数です。例えばn=5の場合は以下の7通りがあります。

5
4 + 1
3 + 2
3 + 1 + 1
2 + 2 + 1
2 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1

とどのつまりこれは、硬貨支払い問題と同じです。5円を1円玉、2円玉、3円玉、4円玉、5円玉の組み合わせで支払う方法は7通りという訳です。従って以前書いた方法と全く同じアルゴリズムで計算できます。

Problem 76: 100を2つ以上の自然数の和で表す方法の数を求めよ

100円を1,2,...,99円玉で表す方法が答えです。よって硬貨支払い問題と同じ漸化式を使うと以下のようになります。a[k][n]はnをk以下の和で表す方法の数です。

class Array
    def [](i)
        i < 0 ? 0 : at(i)
    end
end

N = 100
a = (0..N).collect { [] }
(0..N).each do |n|
    t = a[1][n] = a[1][n-1] + ((n == 0) ? 1 : 0)
    (2..N).each do |k|
        t = a[k][n] = a[k][n-k] + t
    end
end
puts a[99][100]

実行時間は0.01sくらいです。

Problem 77: 素数のみの和で表す方法が5000通り以上となる最初の数は何か？

2,3,5,7,11,13,..円硬貨で支払う方法の数と考えれば全く同じです。金額の上限は適当に決める必要があります。

class Array
    def [](i)
        i < 0 ? 0 : at(i)
    end
end

#上限を適当に決める
N = 100

# 素数のふるいをつくっておく
sieve = []
2.upto(N) do |p|
    next if sieve[p]
    (2*p).step(N,p) {|k| sieve[k] = true}
end

a = (0..N).collect { [] }
(0..N).each do |n|
    t = a[2][n] = a[2][n-2] + ((n == 0) ? 1 : 0)
    (3..N).each do |k|
        next if sieve[k] # kが合成数の時をスキップ
        t = a[k][n] = a[k][n-k] + t
        if a[k][n] > 5000
            puts n
            exit
        end
    end
end

実行時間は0.01sです。

この考え方は分かりやすくて良いのですが、メモリを多く使用するという欠点があります。そこで役に立つのがオイラーの五角数定理です。これは

というものです。
nの整数分割の数p(n)の母関数は

となるので、五角数定理を使えば

となります。これを展開して係数比較をすれば、分割数の漸化式が作れます。
Problem 78はこの方法で解けました。まだ計算時間が掛かっているのでもっと良い方法があるかもしれません。

Problem 78: 分割数が初めて1,000,000の倍数となる整数を求めよ

p = [1]
1.upto(1/0.0) do |n|
    p[n] = 0
    1.upto(1/0.0) do |k|
        if (m = n - k*(3*k+1)/2) >= 0
            p[n] += p[m] * (2*(k%2)-1)
        end
        if (m = n - k*(3*k-1)/2) >= 0
            p[n] += p[m] * (2*(k%2)-1)
        else
            break
        end
    end
    if p[n] % 1000_000 == 0
        puts n
        exit
    end
end

実行時間は41.5sでした。

トポロジカルソート(Problem 79)

ある長さ不明の数列がある。その長さ3の部分数列が
319
680
180
690
129
...(略)
となるとき、もとの数列として可能な物で最も短い物を求めよ

これは仮にもとの数列に同じ数が複数回出現しないなら、トポロジカルソートの問題です。
そこで、まずGraphvizでグラフを描いてみました。DOT言語で記述します。

digraph problem79 {
    3 -> 1 -> 9
    6 -> 8 -> 0
    1 -> 8 -> 0
    6 -> 9 -> 0
    1 -> 2 -> 9
...
}

この絵から答えは一目瞭然でした。
一応Rubyでトポロジカルソートを行うコードも載せておきます。もし、グラフにループがあれば無限ループになってしまう非常に雑なコードですが..。

file = open("problem79-keylog.txt")
# グラフを作る
$graph = (0..9).collect {Array.new(10,false)}
$used = []
while line = file.gets
    x, y, z = line.split(//).map {|v| v.to_i}
    $used[x] = $used[y] = $used[z] = true
    $graph[x][y] = $graph[y][z] = true
end

# トポロジカルソート
$visited = []
def visit(v)
    return if $visited[v]
    $visited[v] = true
    0.upto(9).each do |s|
        next if not $used[s] or not $graph[s][v]
        visit(s)
    end
    puts v
end
0.upto(9).each {|v| $used[v] && visit(v)}

実行時間は0.01s。

整数探索に直す(Problem 80)

平方数でない100未満のnについて
√nの最初100桁の数の和
の和を求めよ

開平法という手もありますが実装が面倒です。今回は100桁と分かっているので、もっと簡単な整数の探索問題に直しちゃう事ができます。つまりnが100未満ならば

を満たす整数kがその最初の100桁分です。ということで、以下の様に解いてみました。

sum = 0
2.upto(99) do |a|
    next if Math.sqrt(a).ceil**2 == a
    # 二分探索
    n = a*10**198
    l = 10**99
    r = (a+1)*10**99
    while r - l > 1
        t = (r+l)/2
        t**2 - n > 0 ? r = t : l = t
    end
    # 桁の和を取る
    while l > 0
        sum += l%10
        l /= 10
    end
end
puts sum

実行時間は0.26sでした。

Project Euler(51 〜 73) ブロコット木など

久々にProject Eulerやりました。まだrowlは使える段階にないので、Rubyつかってます。
このあたりから数論の問題がいろいろ出てきて面白かったです。

ぺル方程式(Problem 66)

簡単には

Dが平方数でない整数の時
x^2 - Dy^2 = 1
の整数解を求めよ

という問題。これはぺル方程式といって、ディオファントス方程式の一種です。
以下のページに詳しく理論と解法が紹介されています。連分数展開を使います。
http://aozoragakuen.sakura.ne.jp/suuron/suuron.html

余談ですが、ディオファントス方程式(特にベズー方程式 a x + b y = d)はコンパイラの教科書にも出てきまして、その関係で私は前からぺル方程式の事を知っていました。
二つの配列アクセスa[p*i+q]とb[r*j+s]が同じ場所を参照するかどうかは

a + sizeof(a[0]) * (p * i + q) == b + sizeof(b[0]) * (r * j + s)

が解を持つかどうかで決まります。これはi,jを変数とするベズー方程式になっています。この解を調べる事でループの並列性検査などが出来ます。

オイラーのトーティエント関数(Problem 69, 70)

オイラーのトーティエント関数φ(n)とはnと互いに素なn以下の自然数の数として定義されています。
これはnの素因数分解が

となるとき、

を満たします。nの素因数分解は非常に重いですから、トーティエント関数に関する問題は

1. 素数のリストの上で探索する
2. エラトステネスの篩で計算

といった方法を取ることになると思います。例えば後者に関しては以下のようなコードで2〜Nについて関数の値を求める事が出来ます。

phi = (0..N).to_a
2.upto(N) do |n|
    if phi[n] == n # n is a prime number
        n.step(N, n) {|p| phi[p] = phi[p]*(n-1)/n}
    end
end

ファレイ数列、ブロコット木(Problem 71,72,73)

この3問はファレイ数列についての問題です。
ファレイ数列というのは0以上1以下の既約な分数を並べたものとして定義されます。
例えば分母が8以下の時は

F8 = 0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1

となります。

ファレイ数列の長さ

Problem 72はファレイ数列の長さを求める問題ですが、これはトーティエント関数を用いて

と表せます。分母がkである既約な1未満の分数は、kと互いに疎なk以下の自然数の数と一致するのでこれが成立します。

ブロコット木

Problem 71と73はファレイ数列の一部だけを考える問題ですが、こういう問題ではブロコット木(Stern Brocot tree)が便利です。
ブロコット木というのは
既約な分数の分子同士、分母同士を加える事を繰り返して作られる木で図のようになります(wikipediaより引用)。


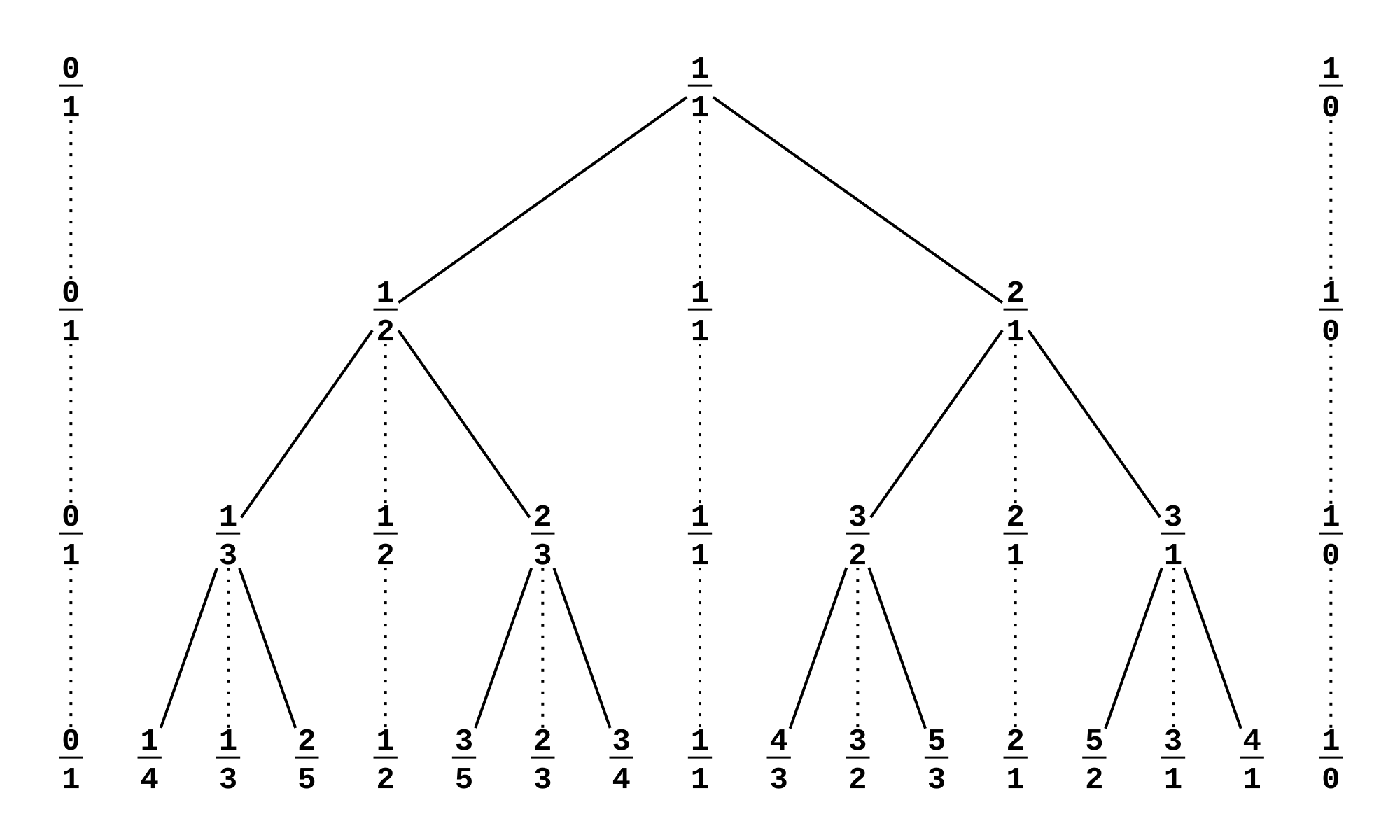
このブロコット木は

• 生成される分数は必ず既約になっている
• 全ての分数を網羅する

という非常に良い性質を持っています。分母分子の約分の問題を考えなくて良いので、既約分数に関する探索問題が高速に解けます。

Problem 71: 分母が1,000,000以下の分数で3/7の未満の最大の物は何か？

3/7を挟む区間でブロコット木を辿って行けば良いです。

la, lb = 0, 1
ra, rb = 1, 2
while true
    ma, mb = la + ra, lb + rb
    if 7*ma < 3*mb
        if mb > 1000000
            puts "#{la}/#{lb}"
            exit
        end
        la, lb = ma, mb
    else
        ra, rb = ma, mb
    end
end

実行時間は0.02sくらいです。

Problem 73: 分母が12,000以下の分数で1/2と1/3の間の数は何個か？

木のノード数を深さ優先探索で求めるだけ。また、分子の数字は考える必要ないです。

def dfs(l, r)
    m = l + r
    return 0 if m > 12000
    dfs(l, m) + dfs(m, r) + 1
end
puts dfs(3, 2)

実行時間は1.83sくらいです。

ここら辺の話はKnuthの本に書いてあったと思います。

コンピュータの数学

rowlの開発を始めて１年が経ちました

1年前の今日、アセンブリで数十行のechoプログラムを作成しました。
それを徐々に育てて、今日ではソースコード行数がトータルで1万5千行を超えていました。
１年でたったこれだけかという気がしなくもないですが、趣味プログラムにしてはそれなりに進んだのかなと思います。
当初の計画通りアセンブリ言語以外の既存言語は実装に使用していません。
これまでの成果をまとめます。

• コンパイラの実装は第２世代まで終了し、現在第３世代の実装を開始しています。
• スタックマシン型のVMが動作しています。
• コピーGC(Mostly Copying-GC)が動作しています。
• (バイトコードの)JITアセンブラが動作しています。
• バイトコードのリンカを作成しました。分割コンパイルが可能です。
• バイトコードのディスアセンブラを作成しました。
• 第３世代rowl
  • レキサ・パーサを作成しました。演算子優先順位法ベースのパーサを採用しました。
  • σ式ベースの正規化された構文木表現を採用しました。
  • パターンマッチングを一部実装しました。JITコンパイラ・アセンブラにより動的にコード生成をしています。

来年の目標

高めに設定しておいて50%くらい達成できればよいかなぁと。

• 最適化の実装に取り組む
  • コンパイラ最適化理論が私の専門なので力を入れたい所。
• 第３世代の実装を終了し、第４世代の実装を始める。レジスタマシン型VMにし、ネイティブJITで動かす。
• REPLを作る。
• メタプログラミング機能に取り組む
  • 力を入れたい部分です。σ式を採用した目的は構文木を柔軟に取り扱い為。
  • 現状では実行時に構文を定義する所までできます。
• アセンブラを自作する
  • 現在はまだGNU Assemblerを使用してるけど(1)ネイティブJITの開発の為(2)x86機械語の勉強の為に、x86アセンブラを自作しようと思っている。
• ビルドシステムを自作する
  • 現在はmakeを使っているけど、せっかくなのでこれも自作する。
• 標準ライブラリの実装を開始する
  • 多倍数整数や浮動小数点数、文字列、各種コンテナ・アルゴリズムなど。
• メタプログラミングライブラリの実装を開始する
  • 実行時構文定義・実行時コード生成を使った面白いライブラリの開発に取り組みたいと思っている。今は以下の物に興味がある。
  • lex/yacc。外部ツールとしてではなく、"import lex"といった感じでプログラム中でimportして使えるような物を作りたい。また、これは第４世代rowlの実装にも使いたい。
  • ページ記述言語。とりあえずはPostScriptを生成できるようにしてみたい。構文木やフローグラフの図示などをしたい。あと、Project Eulerとかの説明で使う絵とかいろいろ使えれば面白い。
  • グラフ記述言語。Graphvizのような物。
  • コンピュータ代数。これは純粋に興味があるので作ってみたい。import algebraとか書いてREPLが数式処理システムに化けたら素敵ではないかという妄想。
• C言語等の他言語で書かれたコードの呼び出し。
  • やっぱり既存資源の活用は大事だと思う。
  • ただし、当初のポリシーを守るためrowl本体・標準ライブラリは他言語に依存しないものにする。
• rowl紹介用のWebページを作る。あとマニュアル。
• 勉強会かなんかでrowlを紹介する。せっかくなのでプレゼンテーションツールをrowlで実装する。

Project Euler (13〜50)

50問目まで解きました。数学を使って工夫すると速く解けたりするようなものについてだけ自分の解答を書きます。

Problem 15

20x20のグリッドの左上から右下までの最短経路数を求めよ

これは２項係数、

の値を計算すれば良いです。２項係数の値はパスカルの三角形の値を上から下へ計算していく方法が効率的です。つまり、以下の漸化式を使います。

コードは次のようになります。

a = [1,1]
2.upto 40 do |n|
    n.downto 0 do |k|
        a[k] = (k == 0 || k == n) ? 1 :
            a[k-1] + a[k]
    end
end
puts a[20]

a[k]の計算にa[k-1]を使いますから、内側のループはdowntoです。

Problem 21,23

Problem 21: 10000以下の全ての友愛数の和を求めよ
Problem 23: 2つの過剰数の和で表されない数の和を求めよ

友愛数も過剰数も約数の和を用いて判定します。約数の和はNの因数分解が

の時

で求まるわけなので、Problem 12と同様にして高速に求める事ができます。
例えばProblem 21の場合は以下の様な感じになります。

N = 30000
d = Array.new(N+1,1)
exp = Array.new(N+1)
2.upto(N) do |n|
    if d[n] == 1 then
        exp.fill(0)
        n.step(N, n) do |k|
            exp[k] = exp[k/n] + 1
            d[k] *= (1-n**(exp[k]+1))/(1-n)
        end
    end
end
sum = 0
2.upto(10000) do |n|
    a = d[n]-n
    b = d[a]-a
    sum += n if a != b && b == n
end
puts sum

実行時間は0.36秒程度です。

Problem 26

1/dの循環節の長さが最大となるようなd (< 1000)を求めよ

循環節の長さをkとすると

が整数となるわけなので

が成立するようなkを調べれば良いです。

Problem 27

n^2 + an + b (n=0,1,2,...)が生成する素数列が最長となるようなa,b(|a|<1000,|b|<1000)を求めよ。

n=0で素数である必要があるからbは素数。
n=1で素数である必要があるから1+a+bは素数。従ってaは奇数で、さらに1+a+b > 0。などの必要条件を調べて探索範囲を絞れば良いです。

N = 20000
sieve = []
primes = []
2.upto(N) do |n|
    next if sieve[n]
    primes.unshift(n) if n < 1000
    (2*n).step(N,n) {|k| sieve[k] = true}
end
max_len = 0
max = 0
primes.each do |b|
    break if b <= max_len
    (-b+2).step(999,2) do |a|
        next if sieve[1+a+b]
        n = 0
        while true
            p = n*n + a*n + b
            break if p < 0 || (p < N && sieve[p])
            raise "N is too small" if p >= N
            n+=1
        end
        max, max_len = a*b, n if n > max_len
    end
end
puts max

実行時間は0.40秒。

Problem 28

下の様にして螺旋状に並べた1001x1001の数字列の、対角にある数の和を求めよ。

21 22 23 24 25
20  7  8  9 10
19  6  1  2 11
18  5  4  3 12
17 16 15 14 13

群数列として考えて、一辺の長さが2*n+1の時の和の一般項を求めると

なのでつまり

にn=500を代入して終わり。

Problem 31

1ペンスから1ポンド硬貨までを使って、2ポンドを支払う方法は何通りか？

以前書いたようにして漸化式を立てる。

Problem 39

p = a + b + cかつa^2+b^2=c^2
である自然数a,b,cを考える。最も解の数が多くなるpの値を求めよ。

これはProblem 9と同じく２元２次不定方程式の問題なので探索は不要。cを消去して因数分解すると

となるので、まずpは偶数であることが必要。ここでa <= bとすればp-a >= p-bだから

の範囲でp^2/2の約数となるp-aの個数を数えれば良いです。

max = 0
max_p = 0
4.step(1000,2) do |p|
    count = 0
    Math.sqrt(p*p/2).ceil.upto(p) do |k|
        count += 1 if (p*p/2)%k == 0
    end
    max, max_p = count, p if max < count
end
puts max_p

実行時間は0.08秒。

Problem 40

0.123456789101112131415161718192021...
のような無限小数の少数第n位をdnとして
d1 * d10 * d100 * d1000 * d10000 * d100000 * d1000000
を求めよ

n桁の数を第n群として群数列的にやればいいです。

r = 1
[1,10,100,1000,10000,100000,1000000].each do |n|
    k, s = 0, 0
    while n > 9*10**k*(k+1)
        n -= 9*10**k*(k+1)
        k += 1
    end
    d = (n-1) % (k+1)
    n = 10**k + (n-1)/(k + 1)
    r *= (n / 10**(k-d))%10
end
puts r

実行時間は0.01秒。

Problem 42,44,45

これらの問題では三角数T(n),五角数P(n)，六角数H(n)を扱いますが、これらは以下のようにして値からインデックスを簡単に求める事ができます。これに基づいて解答を作成すれば上手くできます。

Problem 47

連続する4整数で、全てが4つの素因数からなる数であるものを求めよ

「素因数の数」を使いますが、これもProblem 21,23と同様に反復により求められます。

N = 1000000
sieve = Array.new(N+1, 0)
2.upto(N) do |n|
    if sieve[n] == 0 then
        n.step(N, n) do |k|
            sieve[k] += 1
        end
    end
    if n > 4 && (n-3..n).all? {|k| sieve[k] == 4}
        puts n-3
        exit
    end
end

実行時間は2.75秒。